Linear And Nonlinear System
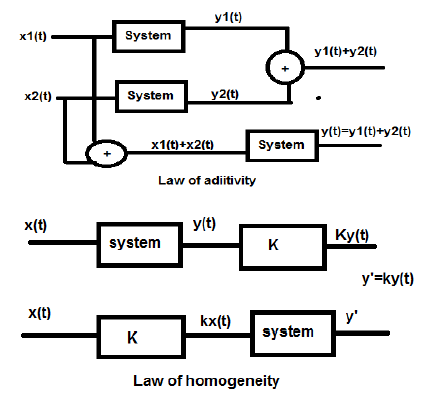
Linear And Non Linear Systems Youtube
Linear and nonlinear system. What is important in considering nonlinear relationships is that a wider range of possible dependencies is allowed. Where x and y are the variables m is the slope of the line and c is a constant value. Any system is called nonlinear that does not satisfy two properties.
Signal and System. There is a difference between a linear and non-linear system. Definition of linear systems2.
Table 5-1 provides examples of common linear and nonlinear systems. Definition of Linear and Non-Linear Equation. Signal and System.
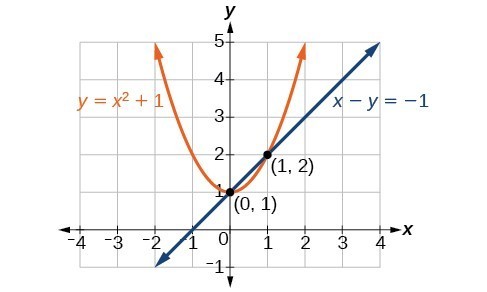
A linear equation forms a straight line on the graph. Our primary concern with these types of problems is the eigenvalue stability of the resulting. I ii Solution.
Examples of Non-linear System. A non-linear equation is such which does not form a straight line. But those for us in European and North American cultures face significant challenges in grasping and describing complex dynamical adaptive systems which is another was.
Here this article gives the information about the example of a linear and nonlinear system to know more details about it. Faxafxay a is a scalar a simple numb. As you go through the lists keep in mind the mathematicians view of linearity homogeneity additivity and shift invariance as well as the informal way most scientists and engineers use static linearity and sinusoidal fidelity.
Linear and nonlinear equations usually consist of numbers and variables. Solved Questions on Linear and Non-Linear SystemsTopics Discussed1.
Output Possibilities Of A A Linear System And B A Nonlinear System Download Scientific Diagram
Linear And Non Linear Systems Solved Problems Part 1 Youtube
Gate Ese Linear And Nonlinear Systems Numericals Offered By Unacademy
5 Examples Of Step Responses Of A A Linear And B A Nonlinear Download Scientific Diagram
Control Engineering Linearization Of Non Linear System 1minute Explanation Youtube
Gate Ese Linear And Nonlinear System Offered By Unacademy
Linear Non Linear Systems Signals And Systems Engineerstutor
The Response In Lfsv For Both The Linear And Nonlinear System Is Download Scientific Diagram
Examples Of Linear And Nonlinear Systems
Alternatives To Linearity
Typical Frequency Response Of A Nonlinear Blue And A Linear System Red Download Scientific Diagram
Gate Ese Lec 15 Linear Non Linear Systems In Hindi Offered By Unacademy
Nonlinear System By Newtonraphson Example Youtube
Solved 2 3 Linear Nonlinear Systems The Linear System Is Chegg Com
Intro To Control 4 3 Linear Versus Nonlinear Systems Youtube
Solutions For Practice In 4 1 Linear And Nonlinear Systems Of Equations 1 Use Substitution
Lecture 11 Systems Of Nonlinear Equations
Linear And Non Linear Equations Lessons Blendspace
Digital Signal Processing Linear Systems
Nonlinear System An Overview Sciencedirect Topics
Gate Ese Hindi Linear And Non Linear System Offered By Unacademy
Nonlinear Systems By Amit Kumar Issuu
Linearization Of A Non Linear System Stack Overflow
Search Q Time Invariant System Tbm Isch
Ppt Ch 2 4 Differences Between Linear And Nonlinear Equations Powerpoint Presentation Id 5177850
7 1 Linear And Nonlinear Systems Of Equations Ppt Download
Nonlinear Control Wikipedia
Methods For Solving A System Of Nonlinear Equations College Algebra
Nonlinear Control Wikipedia
Sc301 Linear And Nonlinear Systems Mech Damp Blog
Nonlinear Model Standardization For The Analysis And Design Of Nonlinear Systems With Multiple Equilibria Springerlink
System Of Equations
Non Linear Systems
Signals Systems Linear None Linear System Youtube
Displacements Of Both Linear And Nonlinear Systems Are In The Same Range Download Scientific Diagram
Sampled Data Models For Linear And Nonlinear Systems Springer Nature Outros Livros Magazine Luiza
Gate Ese Static And Dynamic System Numerical Linear And Nonlinear System Offered By Unacademy
Split Of A Nonlinear System Into Linear And Nonlinear Blocks Download Scientific Diagram
Electrical Systems Linear And Nonlinear Systems In Electrical Engineering
Feedback Control Of Linear And Nonlinear Systems Springer Nature Outros Livros Magazine Luiza
Nonlinear Physics Textbook R C Hilborn Chaos Nonlinear Dynamics 2 Nd Ed Oxford Univ Press 94 00 References R H Enns G C Mcguire Nonlinear Ppt Download
Linear And Nonlinear Systems With Examples Linear Vs Nonlinear Systems Linearity And Superposition Youtube
Non Linear Systems
Mathematical Methods For Scientists And Engineers Linear And Nonlinear Systems Amazon Com Br
Pdf The Applications Of The Non Linear Equations Systems Algorithms For The Heat Transfer Processes
Irrelevance Of Linear Controllability To Nonlinear Dynamical Networks Nature Communications
الجزء الاول Linear And Non Linear Systems Youtube
Mathematics Of Linear And Nonlinear Systems For Engineers And Applied Scientists Amazon Com Br
Time Variant
Nonlinear relationships in general are any relationship which is not linear.
The best example of a linear element is an ordinary resistance. Definition of nonlinear systems3. Linear System A system is said to be linear if superposition principle is applicable to the system. Recall that an ODE is stiff if it exhibits behavior on widely-varying timescales. Signal and System. Implicit Methods for Linear and Nonlinear Systems of ODEs In the previous chapter we investigated stiffness in ODEs. Table 5-1 provides examples of common linear and nonlinear systems. Faxafxay a is a scalar a simple numb. A great many systems are approximately linear if we look at them the right way.
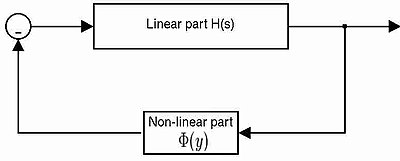
Non-linear Systems We can simply define nonlinear control system as all those systems which do not follow the principle of homogeneity. Signal and System. Because linear equations are so much easier to solve than nonlinear ones much research across a range of disciplines is devoted to finding linear approximations of nonlinear phenomena. Faxafxay a is a scalar a simple numb. A great many systems are approximately linear if we look at them the right way. What is important in considering nonlinear relationships is that a wider range of possible dependencies is allowed. Our primary concern with these types of problems is the eigenvalue stability of the resulting.
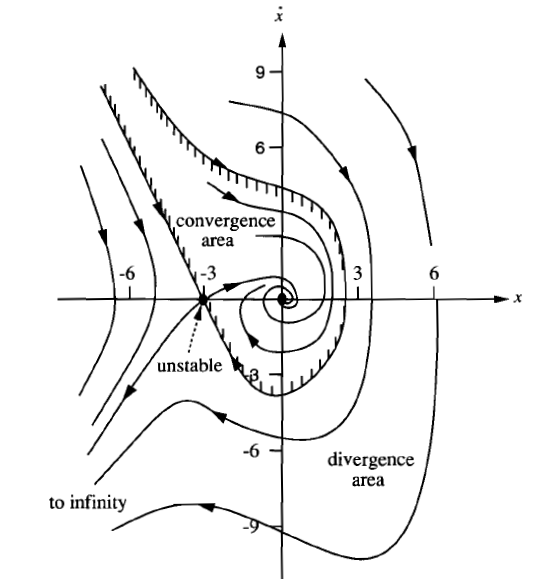
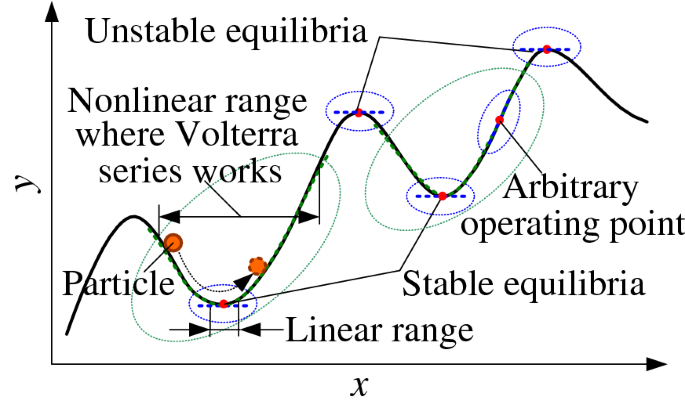
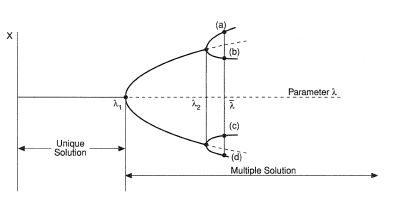
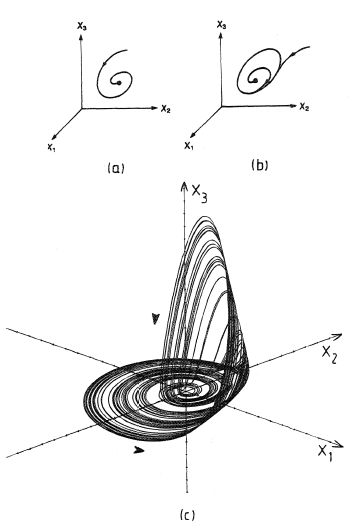
Post a Comment for "Linear And Nonlinear System"